IEEE 754 标准的一些理解
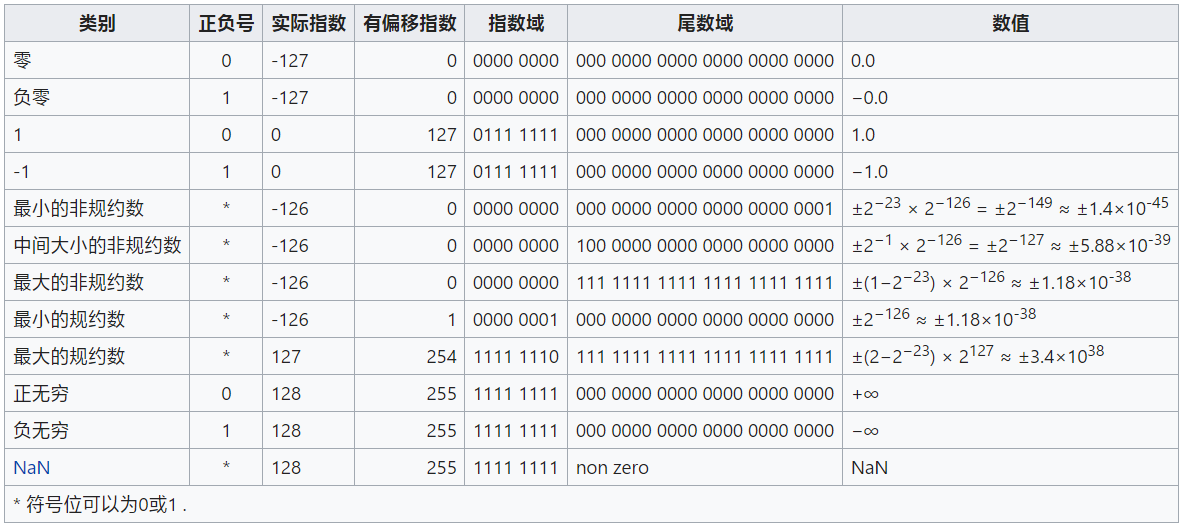
下表以单精度(32位)位的浮点数为例
IEEE754规定了5种数,他们分别是
这个标准是对于浮点数格式的规定。下图是浮点数表示的图示

下图是单精度(32位)浮点数的表示图示

如图所示,在IEEE754标准中,一个单精度浮点数分为3个部分:
符号位
S:1位,表示正负阶码域
E:8位,此处表示移码后的指数,即 \(e=E-127\)尾数域
M:23位,这个地方需要解释一下,在科学计数法中,尾数分为整数部分和小数部分,如 \(5.20\times10^{1314}\),\(5.20\) 是尾数,\(5\) 是整数部分,\(20\) 是小数部分。IEEE754主要做了一件事,就是规定了小数点的位置。我们课本上说:
由于规格化的浮点数的尾数域最左位(最高有效位)总是1,故这一位经常不予存储,而认为隐藏在小数点的左边。
在
IEEE754中确实是这样,尾数的整数部分确实是被隐藏起来了,并且还有一个规定:规格化浮点数中,隐藏起来的整数部分默认为1
非规格化浮点数中,隐藏起来的整数部分默认为0
现在我们来看看那个表,课本上那个表有一些错误,正确的表如下:
| 指数 | 尾数 | 表示的对象 |
|---|---|---|
| 0 | 0 | 正负零 |
| 0 | 非0 | 非规格化正负浮点数 |
| 1~254 | 任意数 | 规格化正负浮点数 |
| 255 | 0 | 正负无穷 |
| 255 | 非0 | NaN(不是一个数) |
整体解释一下:
这个其实就是一个表示数字的系统,需要表示的数字有5种(一开始说的那五种),对于单精度32位来说,就是要把这32位二进制数字进行分配,使得分配完它能够合理地表示出这5种数。
正负零 ,我们很容易想到,只要让指数和尾数都是0,就可以表示正负零了。
正负无穷,既然正负零表示的时候用的是指数尾数都是0,也就是最小,那么无穷的表示肯定得用最大了,所以先让指数最大,阶码为255(对应指数 \(e=128\) )无穷和0一样,只要一个数就够了,那就让尾数为0,这样比较方便。
NaN,这个东西表示它不是一个数,而是出现了无效或错误,那就把它放在指数为 255 的部分吧,并且这个部分正负无穷占去了尾数为 0 的一个,剩下的留着也没用,分给规格化浮点数、非规格化浮点数 又有点磕碜,毕竟对于这种尾数域每一个数都有意义的,要分就把一整段全都分过去,这缺了一个,不太合适。那就全给它吧,所以指数为 255 的时候,尾数 非零 就都表示 NaN
非规格化正负浮点数,这个是用来表示一些绝对值非常非常小的数。规格化浮点数尾数部分的取值范围是 \([1,2)\) ,有些数就表示不出来,那就用非规格化浮点数表示。IEEE754对于这个东西搞了很多特殊,前面说了,它那省略掉的整数部分默认是0,也就是说它的尾数取值范围是 \((0,1)\),同时还让它在移码时候的偏移值\(-1\),比如在单精度浮点数中,偏移值是127,\(E=0的时候,e=-127\),但对于它,\(E=0,但e=-126\) 。这样做的目的,就是为了让它能表示规格化浮点数表示不了的那些太小的数。因为我们知道,规格化浮点数的绝对值最小值是“阶码域为1,尾数域为0”的时候,也就是 \(1.0\times2^{-126}\) ,非规格化浮点数就是来表示像 \(0.520\times2^{-126}\) 那样的数,所以才让它的 \(e=-126\)
规格化正负浮点数,上面说完,这个应该就不用说了。就把剩下的阶码域1~254都分给他,让它好好表示就行。
下表是IEEE754 中单精度(32位)浮点数的一些特殊值(其实就是表示范围)